SGP-Bench
Characterizing the capabilities of LLMs is important to understand what matters and what needs to be improved. Assessing their capabilities, however, can be challenging, in part because it is hard to find tasks to which they have not been exposed during training. To address this, we turn to symbolic graphics programs, which are a popular representation for graphics content that procedurally generates visual data. Large language models (LLMs) have shown exciting promise towards program synthesis, but do they "understand" symbolic graphics programs? Unlike conventional programs, symbolic graphics programs can be translated to graphics content (e.g., 2D images, 3D geometry). Here, we characterize an LLM's "understanding" of symbolic programs in terms of their ability to answer questions related to the graphics (spatial) content. This task is challenging as the questions are difficult to answer from the symbolic programs alone -- yet, they would be easy to answer from the corresponding graphics content as we verify through a human experiment. To understand symbolic programs, LLMs may need to possess the ability to "imagine" how the corresponding graphics content would look without visually seeing it. We use this task to evaluate LLMs by creating a large benchmark for the semantic understanding of symbolic graphics programs. This benchmark is built via a novel usage of program-graphics correspondence, hence requiring minimal human efforts. We evaluate both commercial and open-source LLMs on our benchmark to elucidate a preliminary assessment of their ability to reason about visual scenes from programs. We find that this task well distinguishes existing LLMs and models that are considered good at reasoning perform better.
Lastly, we introduce a way to improve this ability - Symbolic Instruction Tuning (SIT). Specifically, we query powerful vision-language models (e.g., GPT-4o) with questions and images generated by symbolic programs. These program-question pairs are collected as our instruction dataset which is then used to finetune an LLM. With a small amount of data, we find that SIT can improve the understanding of LLMs regarding symbolic graphics programs. Assessing how well models “understand” symbolic graphics programs offers new possibilities for LLMs to perform visual reasoning. Finally, we showcase such possibilities in generic instruction tuning.
SGP-Bench
| Reset | Size | Date | Overall | Semantics | Count | Color | Shape | Reasoning |
| GPT-4o-2024-08-06 | - | 2024-08-06 | 64.8 | 45.9 | 56.8 | 87.3 | 75.2 | 50.4 |
| GPT-4o-2024-05-13 | - | 2024-05-13 | 63.3 | 78.7 | 55.3 | 83.2 | 69.6 | 47.1 |
| GPT-4o mini-2024-07-18 | - | 2024-07-18 | 58.5 | 39.8 | 50.4 | 79.1 | 70.9 | 41.4 |
| GPT-4 Turbo-2024-04-09 | - | 2024-04-09 | 60.9 | 76.4 | 53.9 | 83.2 | 68.7 | 41.2 |
| GPT-3.5 Turbo-01-25 | - | 2024-01-25 | 49.8 | 31.9 | 45.1 | 72.9 | 57.7 | 33.8 |
| Claude 3 Haiku-2024-03-07 | - | 2024-03-07 | 48.6 | 26.4 | 39.8 | 75.0 | 61.0 | 30.1 |
| Claude 3 Sonnet-2024-02-29 | - | 2024-02-29 | 56.5 | 37.5 | 50.3 | 80.3 | 65.7 | 39.5 |
| Claude 3.5 Sonnet-2024-06-20 | - | 2024-06-20 | 67.4 | 50.5 | 58.4 | 89.1 | 75.8 | 52.7 |
| Gemma-1.1-2B-IT | 2B | 2024-06-03 | 31.7 | 32.1 | 33.3 | 25.0 | 35.6 | 28.7 |
| Gemma-1.1-7B-IT | 7B | 2024-06-03 | 39.3 | 34.7 | 27.5 | 45.3 | 52.3 | 29.9 |
| InternLM2-7B | 7B | 2024-07-28 | 38.2 | 27.9 | 32.4 | 57.0 | 43.1 | 29.9 |
| InternLM2-20B | 20B | 2024-07-28 | 42.4 | 25.5 | 37.9 | 62.3 | 48.3 | 27.6 |
| InternLM2.5-7B | 7B | 2024-07-28 | 42.1 | 27.3 | 31.7 | 59.8 | 51.5 | 28.2 |
| Mistral-7B-v0.3 | 7B | 2024-06-03 | 41.7 | 30.4 | 32.4 | 62.4 | 47.0 | 29.6 |
| Mistral-NeMo-12B | 12B | 2024-07-25 | 44.9 | 29.6 | 35.5 | 65.2 | 54.8 | 29.6 |
| Mistral-Large2-12B | 123B | 2024-07-25 | 57.2 | 38.9 | 55.8 | 81.4 | 63.5 | 40.8 |
| Yi-1.5-9B | 9B | 2024-06-03 | 35.5 | 30.9 | 40.4 | 49.3 | 29.7 | 30.1 |
| Yi-1.5-34B | 34B | 2024-06-03 | 44.3 | 30.8 | 36.4 | 64.4 | 52.3 | 23.4 |
| Aya-23-8B | 8B | 2024-07-30 | 29.0 | 24.4 | 25.5 | 34.3 | 32.6 | 25.9 |
| Aya-23-35B | 35B | 2024-07-30 | 44.2 | 30.7 | 35.4 | 64.8 | 51.1 | 31.8 |
| Command R-35B | 35B | 2024-06-03 | 46.1 | 31.1 | 44.2 | 67.6 | 49.5 | 34.1 |
| Command R-104B | 104B | 2024-07-30 | 50.0 | 33.9 | 44.9 | 72.7 | 56.5 | 34.1 |
| Qwen-1.5-7B | 7B | 2024-06-03 | 37.6 | 22.6 | 31.7 | 56.3 | 47.1 | 23.4 |
| Qwen-1.5-32B | 32B | 2024-06-03 | 49.4 | 30.7 | 50.1 | 71.3 | 55.2 | 31.0 |
| Qwen-1.5-72B | 72B | 2024-06-03 | 46.6 | 29.9 | 31.9 | 69.8 | 59.8 | 26.5 |
| Qwen-1.5-110B | 110B | 2024-06-03 | 49.9 | 32.4 | 43.1 | 73.4 | 56.0 | 33.2 |
| Qwen-2-72B | 72B | 2024-07-25 | 53.7 | 37.3 | 42.6 | 77.0 | 63.0 | 37.2 |
| Llama3-8B | 8B | 2024-06-03 | 42.9 | 30.4 | 37.2 | 62.6 | 48.4 | 29.3 |
| Llama3-70B | 70B | 2024-06-03 | 54.8 | 36.4 | 49.6 | 74.9 | 64.5 | 36.9 |
| Llama3.1-8B | 8B | 2024-07-25 | 46.5 | 33.9 | 38.5 | 66.7 | 53.3 | 26.8 |
| Llama3.1-70B | 70B | 2024-07-25 | 57.4 | 40.0 | 54.3 | 78.8 | 65.9 | 41.1 |
| Llama3.1-405B | 405B | 2024-07-30 | 58.0 | 37.6 | 58.4 | 81.6 | 64.7 | 38.9 |
| Reflection-Llama3.1-70B | 70B | 2024-09-08 | 47.4 | 34.8 | 39.3 | 64.6 | 55.8 | 34.3 |
| DeepSeek-Coder-V2-16B | 16B | 2024-07-25 | 45.1 | 30.9 | 37.9 | 63.7 | 54.8 | 26.8 |
| CodeQwen1.5-7B | 7B | 2024-06-03 | 30.1 | 24.5 | 26.2 | 34.4 | 38.7 | 24.5 |
| Mistral-Codestral-22b-v0.1 | 22B | 2024-06-03 | 49.1 | 30.9 | 44.6 | 69.8 | 58.1 | 32.1 |
| Random Choice | - | 2024-06-03 | 25.9 | 25.3 | 25.9 | 27.1 | 25.2 | 26.8 |
Overall results of different models on the SGP-Bench (SVG). The best-performing model in each category is in-bold.
Large language models (LLMs) are exposed to vast amounts of online data, including open-access SVG data. To investigate whether their semantic understanding ability is due to potential data leakage, we propose a semantic consistency test by introducing global translations or rotations to SVG graphics, ensuring SE(2) invariance. Such spatial interventions fundamentally alter the code representation, as SVG graphics consist of lines and Bezier curves with anchor points, and SE(2) operations change all numerical values in the code. However, the SVG's semantics—such as shape or color—remain unaffected by this perturbation. This allows us to examine how LLMs respond when the same vector graphics are presented with drastic code-numerical changes. If the model maintains consistency under these conditions, it suggests that the semantic understanding is likely based on a fundamental level of comprehension or visual imagery rather than mere memorization of the code.
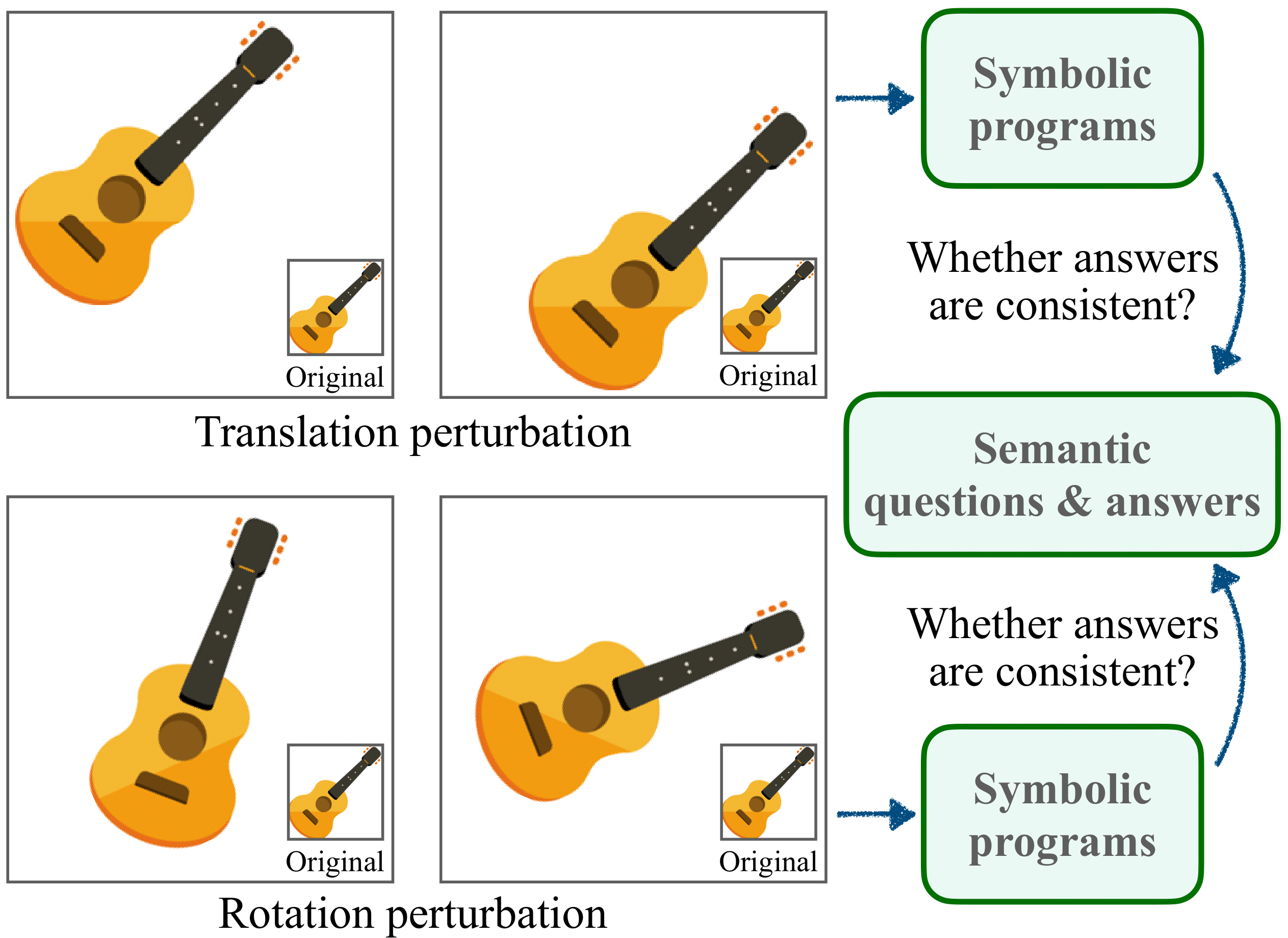
The semantic consistency test assesses if semantic understanding remains the same when the program is perturbed without semantically changing the image content.
Our experiments with the SVG-Invariance benchmark demonstrate that most LLMs exhibit robust semantic understanding of graphics programs under translation (T) and translation + rotation (SE(2)) perturbations. Not only do the models remain consistent in their predictions under perturbations, but their performance on perturbed inputs also shows minimal fluctuation compared to their performance on the SVG-Understanding benchmark. We posit that this indicates that the semantic understanding ability that we evaluate of LLMs is unlikely due to data leakage, but rather, could stem from a potential foundational capability to interpret the semantics of deterministic, symbolic graphics programs.
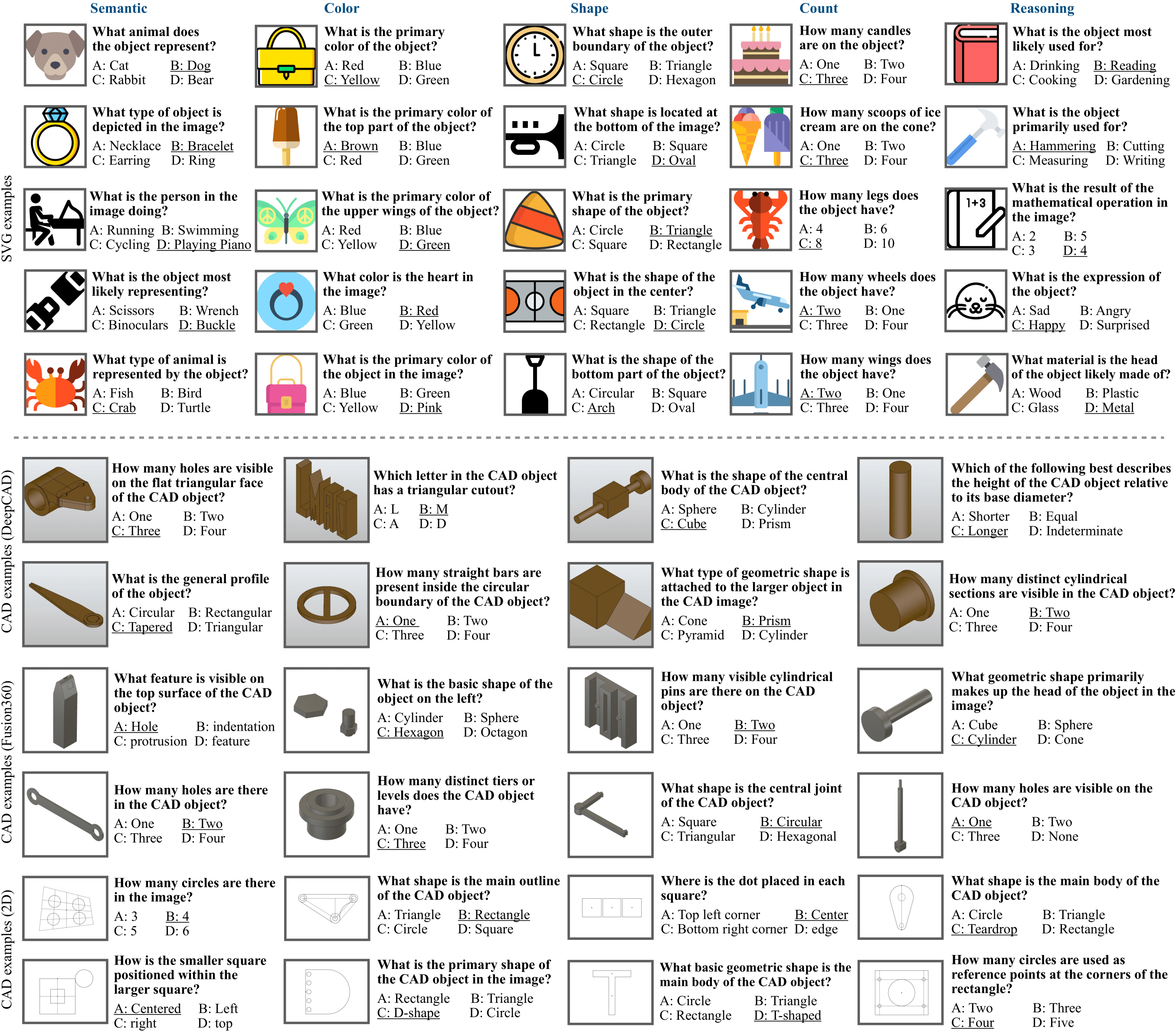
We introduce the task of semantic symbolic graphics program understanding, where our goal is to assess to what extent a LLM is able to understand the symbolic graphics program, which may begin to belie some latent capability to visually imagine. Specifically, we take advantage of the correspondence between symbolic graphics programs and rendered images, and then we characterize the understanding of symbolic graphics programs as the semantic understanding of the corresponding rendered image. To do so, we use the performance on question-answering to evaluate the semantic understanding of images. The same set of questions, along with the corresponding symbolic graphics programs, are then used to evaluate the symbolic program understanding of LLMs. A brief illustration of symbolic graphics program understanding is given in the following figure. The intuition behind this evaluation is that, if an LLM really has a good sense of the symbolic graphics, then the LLM should have a rough understanding about its rendered image such that it is able answer arbitrary semantic questions regarding this rendered image.
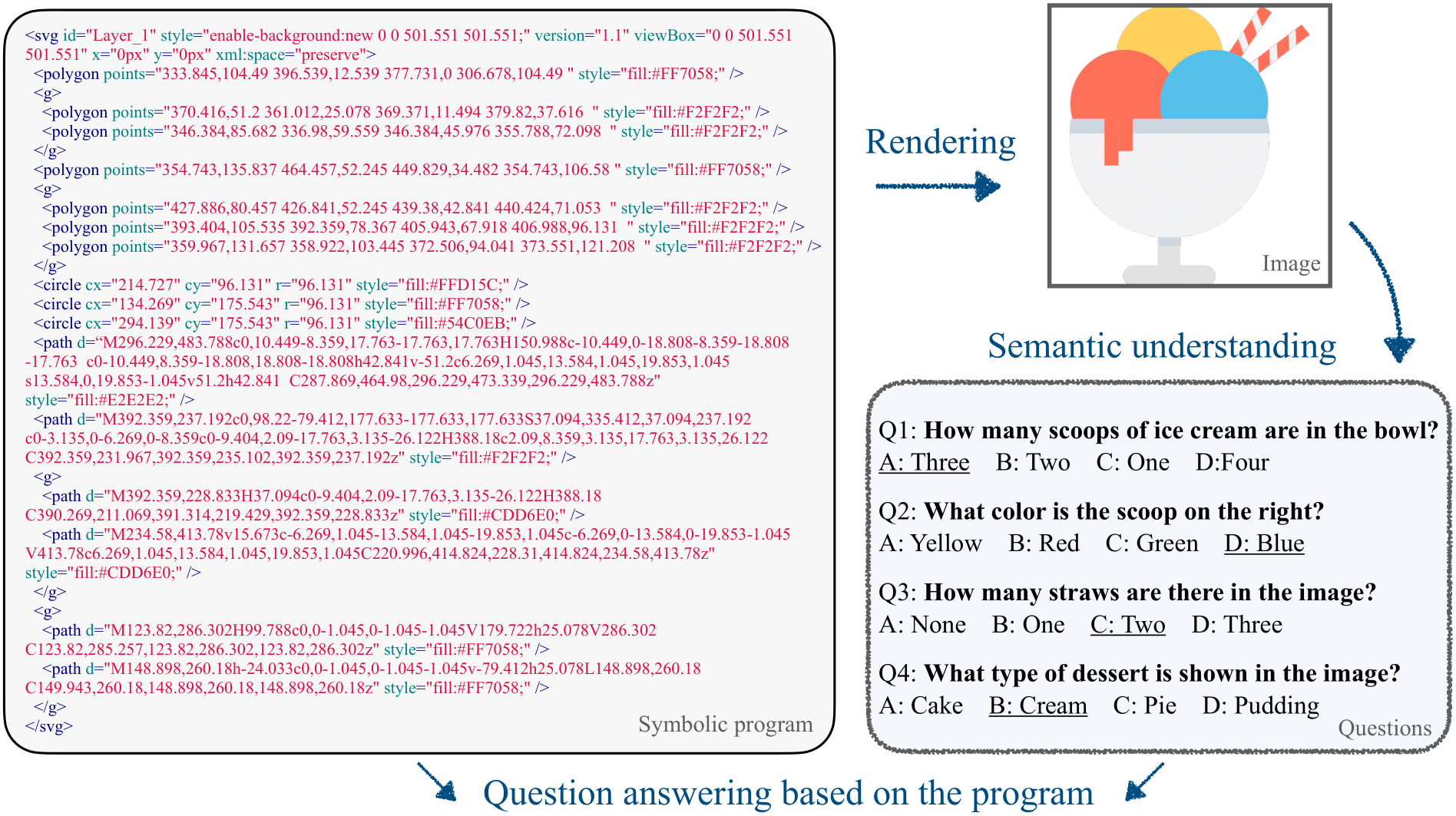
Symbolic graphics program understanding can also be viewed as a form of visual question answering in the sense that visual input is represented by a symbolic program representation. Compared to existing vision-language models that encodes images with a text-aligned neural encoder, our paper considers the case where the visual input are encoded by a symbolic program that can exactly recover the graphics content. From this perspective, our task aims to study and uncover the potential of using symbolic programs as a representation to perform visual reasoning.
To construct our benchmark, we need questions about a symbolic program based on its rendered image. To build a large benchmark, it is essential that we consider how we can effectively scale up the question collection with minimal human labeling efforts. To this end, we use a powerful large vision-language model (e.g., GPT-4o) to generate many semantic questions based on the rendered images, and then we inspect them manually to make sure that most of the questions are reasonable and the answer to them is also correct. We also run a human study over 500 of the automatically generated questions along with the corresponding images, and find high agreement. The overall procedure for our dataset creation is given in the following figure:
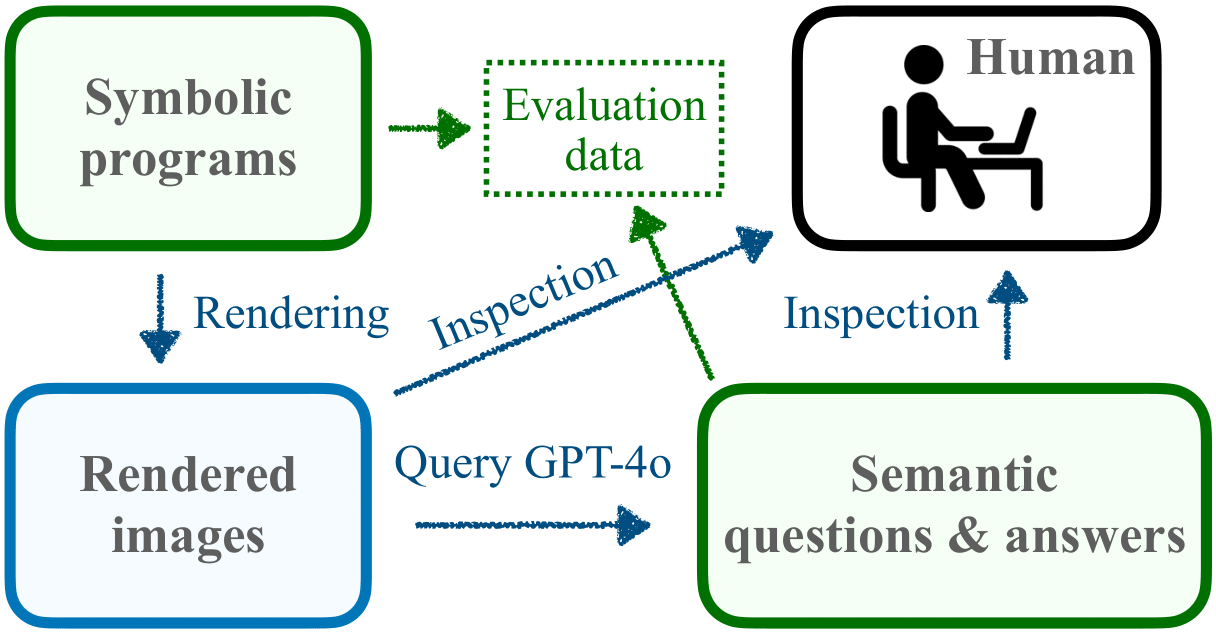
In this pipeline, the rendering of symbolic programs and the GPT-4o querying are both scalable and can be done with minimal human involvement. Human annotators then inspect the generated question-answer pairs based on the rendered image, which requires much less efforts than manually writing questions and answers. We emphasize that this program-question-answer triplet data creation method is general, as it works for most of the symbolic graphics programs. SVG programs can directly produce 2D images, so it is straightforward to use this pipeline. For CAD programs, they produce 3D models and we first render them into 2D images with a few fixed camera positions. These rendered images from different views are then combined together to query GPT-4o, and the following procedures are identical to the SVG case.
Inspired by how visual instruction tuning (e.g., LLaVa) enables large vision-language models to understand images with visual-question-answering (VQA) data, we aim to perform symbolic instruction tuning for LLMs to better bridge the gap between the semantic understanding and the symbolic reasoning within the graphics programs. While there exist no semantic instruction-following datasets directly over symbolic programs, these symbolic graphics programs can be rendered into 2D images with which we can easily query powerful vision-language models (e.g., GPT-4o is used in our case) to obtain a detailed semantic captioning based on the rendered image. The intuition is straightforward, as we want to build an intrinsic connection for LLMs between semantic natural language description and symbolic graphics programs. The instruction data is created in a similar spirit to our benchmark. We leverage the correspondence between symbolic problems and graphics content, and then use the rendered images to obtain semantically rich descriptions. Following this idea, we construct the first semantic description dataset for symbolic graphics programs. Specifically, for each image rendered from a symbolic graphics program, we prompt GPT-4o to produce a detailed and semantically-rich description. Finally, we end up with a dataset that contains semantic descriptions for totally 72K symbolic programs. We generally follow the standard instruction fine-tuning procedure (including the default hyperparameter settings) from Alpaca and use supervised finetuning to train open-source LLMs with our own symbolic instruction data.
Our SIT data can also be used in a reverse fashion (rev-SIT), i.e., rephrasing the answer as the new question and the question as the new answer. See the comparison between original and reverse SIT data in the bellow figure. rev-SIT resembles code instructing tuning data, i.e., given an instruction, generate the corrsponding graphics code. The instruction in rev-SIT would be a text description and the LLM should learn to generate code that when it is rendered, best fit the text description.
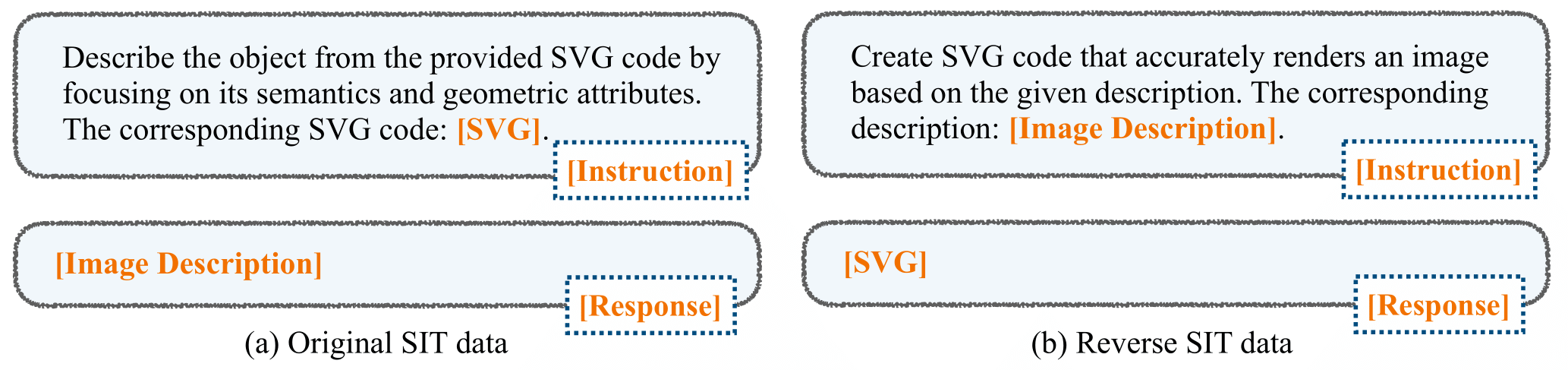
Comparison between original and reverse SIT data.
We evaluate the effectiveness of using SIT data to improve generic instruction tuning performance by mixing additional SIT data into the Open-Instruct data.
| Benchmark | Open-Instruct | Open-Instruct-SIT | Open-Instruct-rev-SIT | Open-Instruct-mixed-SIT |
|---|---|---|---|---|
| XNLI | 41.8 | 43.3 (+1.5) | 43.1 (+1.3) | 42.9 (+1.1) |
| IFEval | 14.8 / 24.9 | 16.3 (+1.5) / 28.9 (+4.0) | 18.3 (+3.5) / 30.5 (+5.6) | 16.6 (+1.8) / 29.6 (+4.7) |
| HellaSwag | 60.0 | 60.2 (+0.2) | 60.5 (+0.5) | 60.4 (+0.4) |
| AGIEval | 23.7 | 30.3 (+6.6) | 31.6 (+7.9) | 29.2 (+5.5) |
| C-Eval | 46.4 | 47.9 (+1.5) | 48.0 (+1.6) | 48.1 (+1.7) |
| BigBenchHard | 59.5 | 60.7 (+1.2) | 60.2 (+0.7) | 61.2 (+1.7) |
| Arithmetic | 89.8 | 91.8 (+2.0) | 90.1 (+0.3) | 91.8 (+2.0) |
| GSM8k | 48.2 | 50.7 (+2.5) | 51.0 (+2.8) | 51.5 (+3.3) |
| CoQA | 67.9 | 69.1 (+1.2) | 68.7 (+0.8) | 69.1 (+1.2) |
| PIQA | 79.9 | 80.3 (+0.4) | 80.3 (+0.4) | 80.4 (+0.5) |
| MMLU | 60.4 | 61.0 (+0.6) | 61.1 (+0.7) | 61.6 (+1.2) |
| MathQA | 39.3 | 40.4 (+1.1) | 40.3 (+1.0) | 40.7 (+1.4) |
| SQuAD2.0 | 28.9 | 28.7 (-0.2) | 31.6 (+2.7) | 29.9 (+1.0) |
| ASDiv | 18.5 | 21.8 (+3.3) | 20.1 (+1.6) | 21.3 (+2.8) |
Is it really easy to answer semantic reasoning questions over symbolic graphics programs? We provide an intriguing experiment to demonstrate that SVG programs can be quite difficult for LLMs to understand such that even if the corresponding rendered images are fairly easy for humans to recognize, all these powerful LLMs still fail dramatically, only reaching a chance-level accuracy. Specifically, we construct symbolic graphics programs that can produce MNIST-like images, as shown in bellow image.
Examples of our SGP-MNIST challenge, hand-written digit constructed by SVG programs.
The symbolic programs that can render MNIST-like images are quite simple, typically only containing 1 or 2 path operations. We introduce the SGP-MNIST challenge where we have 100 symbolic graphics programs per digit (in total 10 digits: 0-9). Therefore, we have 1,000 symbolic graphics programs in total. For each problem, we ask one multiple-choice question (with 10 options of digit 0-9): which digit does the SVG program represent? The results are shown in the bellow table.
| Method | Accuracy (%) |
|---|---|
| Yi-1.5-34B | 5.5 |
| LLama3-70B | 10.0 |
| Qwen-1.5-110b | 10.0 |
| Qwen-2-70b | 11.3 |
| GPT-3.5t | 10.2 |
| GPT-4t | 10.6 |
| GPT-4o | 13.0 |
@misc{qiu2024largelanguagemodelsunderstand,
title={Can Large Language Models Understand Symbolic Graphics Programs?},
author={Zeju Qiu and Weiyang Liu and Haiwen Feng and Zhen Liu and Tim Z. Xiao and Katherine M. Collins and Joshua B. Tenenbaum and Adrian Weller and Michael J. Black and Bernhard Schölkopf},
year={2024},
eprint={2408.08313},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2408.08313},
}